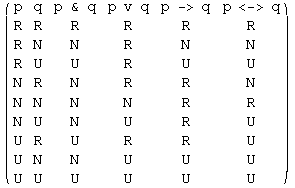Trovrednostna logika
Do zdaj smo se ukvarjali s klasično dvovrednostno logiko. Vsaka izjava je
bila ali resnična ali neresnična. Vrednost sestavljene izjave smo izračunali po
pravilih definicij izjavnih povezav. V programu Hyperproof, ki po
začetnih optimističnih napovedih ni nikoli zaživel v Windows okolju, je postalo
možno nekoliko drugačno izračunavanje resničnostnih vrednosti. Podobno kot pri
programu Svet Tarskega imamo v hyperproofu situacijo, ki bi
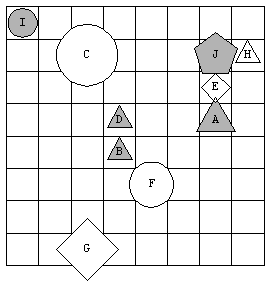
prilagojena naši inačici, to je likom, lahko izgledala takole:
Liki so lahko trikotniki, kvadrati in petkotniki. Kaj pa so I, C in F?
Velik krog pomeni, da je lik velik, ne vemo pa, katere oblike. Temu rečemo, da
je situacija nepopolna. Stavek »Lik C
je trikotnik.« ni ne resničen ne neresničen. Zato bomo rekli, da je njegova
vrednost nedefinirana ali vprašljiva (ali nedoločena), za kar bomo uporabljali
znak U (undefined). V hyperproofu nam nedoločenost pomeni pomanjkanje našega
vedenja, pod krogom se namreč skriva pravi lik.
Kako bomo računali z novo vrednostjo? Kakšna je vrednost stavka: Lik D je
majhen, F pa je srednje velikosti? Tokrat sta oba stavka resnična, zato je
resničen njun stik (konjunkcija). Kaj pa »Lik D je trikotnik in I petkotnik«?
Tokrat je drugi del nedefiniran, zato je tudi celota nedefinirana. Podobno je
»Lik D je trikotnik ali pa je I petkotnik.« resničen, saj je resničen prvi del,
drugega nam sploh ni treba gledati.
Tokrat bomo podali izračun samo za štiri izjavne povezave:
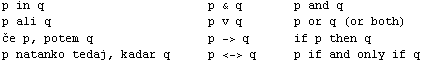
Tabela izgleda takole:
Izključujoči
“ali ali” bomo obravnavali kot negacijo ekvivalence. Za negacijo velja tabela:
ØR = N, ØN
= R, ØU = U.
Opomba: Prvi
sistem trovrednostne logike je vpeljal poljski logik Łukasiewicz. Njegova tabela se malenkostno razlikuje od Kleenejeve pri implikaciji in
ekvivalenci. Lukasiewicz je resnico označeval z 1, neresnico z 0 in nedoločeno
vrednost (pri njem je „možna“) z ½. Njegova tabela je takšna:
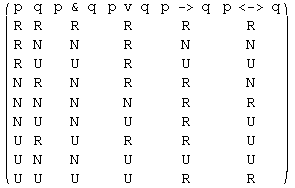
Najenostavnejša trovrednostna logika je Bochvarjeva (l. 1939). Pri njem ima
stavek srednjo vrednost, če v njem nastopa termin, ki nima reference, n.p.
imamo svet Tarskega s tremi liki (A, B, C) stavek pa govori o D. Tak stavek
nima pomena (oz. ni smiselen). Preglednica za to logiko izgleda takole:

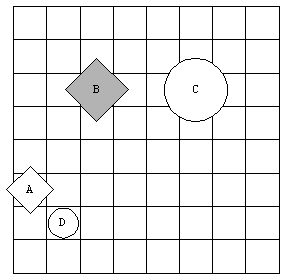
Vrnimo se zdaj k našim
situacijam.
V tem svetu so resnične izjave: Lik A je kvadrat ali lik D ni petkotnik. Če
je lik D petkotnik, potem je C velik. Če je lik B trikotnik, potem je lik C
tudi trikotnik. Dva lika sta velika.
Neresnične so na primer izjave: Lik A je trikotnik in lik D je kvadrat. Lik
D je velik in je trikotnik. Ali je A trikotnik ali je B trikotnik. Samo en lik
je velik.
Nedoločene so izjave: C in D sta trikotnika. B in C sta kvadrata. A je
trikotnik ali pa je D trikotnik. Če je D trikotnik, potem je tudi C trikotnik.
Če je D trikotnik, potem je A petkotnik. Vsi liki so kvadrati. Obstaja vsaj en
trikotnik.
Oba omenjena sistema trovrednostne logike sta razširitvi klasične
dvovrednostne logike v smislu, da če zbrišemo vrstice z U, dobimo klasične
tabele.
Naloge
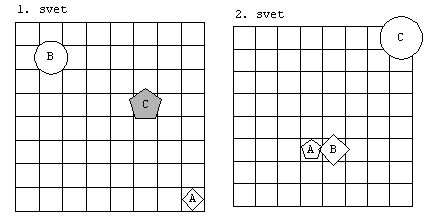
1. Ugotovi
resničnostno vrednost danih stavkov, podanih v 2 svetovih
1. Lik B je
srednje velikosti.
2. Lik B je
kvadrat.
3. Lik A je bel.
4. Lik C je
petkotnik.
5. Lik A je
velik.
6. Lik C je
kvadrat.
7. Lik C je
trikotnik.
8. Lik C je
majhen.
9. Lik B je
velik.
10. Lik C je siv.
11. Lik B je
kvadrat, če in samo če lik A ni srednje velikosti.
12. Lik C ni
majhen ali lik A ni velik.
13. Ali lik C ni
trikotnik ali lik B ni kvadrat.
14. Lik B je
trikotnik, če in samo če lik C ni majhen.
15. Ali lik C ni
srednje velikosti ali lik C ni trikotnik.
16. Lik B ni
kvadrat, če in samo če je lik B bel.
17. Lik B je
srednje velikosti, če in samo če je lik B siv.
18. Če lik A ni
bel, potem lik C ni bel.
19. Če lik B ni
kvadrat, potem lik C ni bel.
20. Lik B ni
kvadrat in lik B je bel.

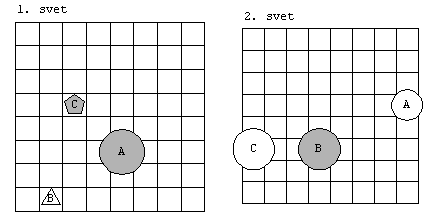
2. Ugotovi resničnostno vrednost danih
stavkov, podanih v 2 svetovih
1. Lik C ni bel,
če in samo če lik A ni kvadrat.
2. Lik A je siv
ali je lik A petkotnik.
3. Lik A je
trikotnik in lik A ni petkotnik.
4. Lik A ni
trikotnik in lik B je srednje velikosti.
5. Lik B je
kvadrat in lik B ni petkotnik.
6. Lik C ni bel
ali lik A ni trikotnik.
7. Ni res, da:
ali je lik C siv ali je lik B kvadrat.
8. Ni res, da:
ali lik C ni trikotnik ali lik C ni petkotnik.
9. Ni res, da:
lik B je kvadrat in lik C je majhen.
10. Obstaja tak
x, da za vsak y velja: lik x je desno od y.
11. Obstaja tak
x, da za vsak y velja: lik x je nad y.
12. Obstaja tak
x, da za vsak y velja: lik x je nad y.
13. Za vsak x
obstaja tak y, da velja: lik x je majhen in lik y je velik.
14. Za vsak x
obstaja tak y, da velja: lik x je petkotnik, če in samo če lik y ni siv.
15. Za vsak x
obstaja tak y, da velja: lik x ni trikotnik in lik y je srednje velikosti.
16. Obstaja tak
x, da za vsak y velja: lik x ni bel, če in samo če je lik y srednje velikosti.
17. Obstaja tak
x, da za vsak y velja: če lik x ni velik, potem je lik y majhen.
18. Obstaja tak
trikotnik x, da za vsak bel lik y velja: lik x je pod y.
19. Obstaja tak
bel lik x, da za vsak bel lik y velja: lik x je pod y.
20. Za vsak siv
lik x obstaja tak kvadrat y, da za vsak bel lik z velja: lik x je desno od y in
lik y je manjši kot z.

Rešitve so
na strani 48!
Zdenka
Oven